- \( G = \{ 3m+2 \,|\, m \in \mathbb{Z} \} = \{ \dots, -4, -1, 2, 5, \dots \} \) with addition.
- \( \mathbb{R}_{<0} \) (negative real numbers) with multiplication.
- \( \mathbb{Q} \) (rational numbers) with subtraction.
- \( G = \{ x \in D_4 \,|\, x \mbox{ is a reflection} \} \) with function composition.
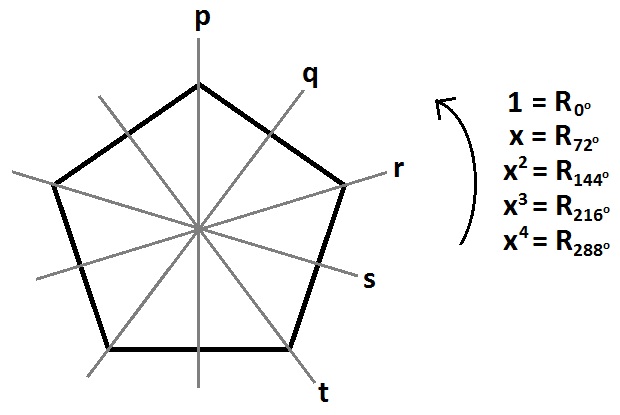
Use the given labels: \(p,q,r,s,t \) for reflections and \( 1,x,x^2,x^3,x^4 \) for the (counter clockwise) rotations. In your table, order the elements as follows: \( 1 \; x \; x^2 \; x^3 \; x^4 \; p \; q \; r \; s \; t \)
Alternate Approach: For those brave enough to try the generator and relation approach, you may list elements as \(1 \; x \; x^2 \; x^3 \; x^4 \; y \; xy \; x^2y \; x^3y \; x^4y \) and use the relations: \( x^5=1 \), \( y^2=1 \), and \( (xy)^2=1 \).