
| > | restart;
with(plots): with(VectorCalculus): |
Warning, the name changecoords has been redefined
Warning, the assigned names `<,>` and `<|>` now have a global binding
Warning, these protected names have been redefined and unprotected: `*`, `+`, `-`, `.`, D, Vector, diff, int, limit, series
rB and rL are radial parameters that determine how "big" and "fat" the
torus is. rB is the distance from the "center" of the torus to the circle
lying in the "center" of the ring. rL is the radius of the "ring" itself.
m determines how many times the curve is to wrap around the torus.
| > | rB := 4; rL := 1; m := 4; |
![]()
![]()
![]()
| > | xc := (phi,theta,r) -> (r*cos(phi)+rB)*cos(theta);
yc := (phi,theta,r) -> (r*cos(phi)+rB)*sin(theta); zc := (phi,theta,r) -> r*sin(phi); |
![]()
![]()
![]()
![]()
![]()
We should make the torus that the curve wraps around slightly smaller than the
curve -- so the curve is on the "outside" of the torus.
| > | sc := 0.95; |
![]()
| > | torusEqn := (sqrt(x^2+y^2)-rB)^2+z^2 = (sc*rL)^2; |
![(Typesetting:-mprintslash)([torusEqn := ((x^2+y^2)^(1/2)-4)^2+z^2 = .9025], [((x^2+y^2)^(1/2)-4)^2+z^2 = .9025])](images/torusTNB_10.gif)
| > | t1 := plot3d([xc(phi,theta,sc*rL),yc(phi,theta,sc*rL),zc(phi,theta,sc*rL)],
phi=0..2*Pi,theta=0..2*Pi,color=grey,scaling=constrained); c1 := spacecurve([xc(m*theta,theta,rL),yc(m*theta,theta,rL),zc(m*theta,theta,rL)], theta=0..2*Pi,color=blue,scaling=constrained,numpoints=5000,thickness=3); |
![]()
![]()
| > | display3d(t1,c1); |

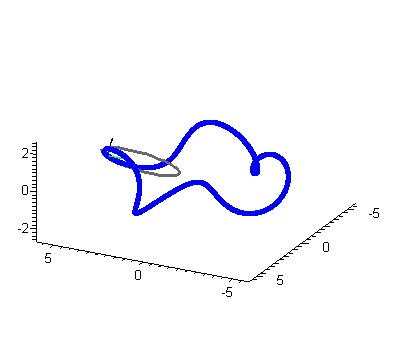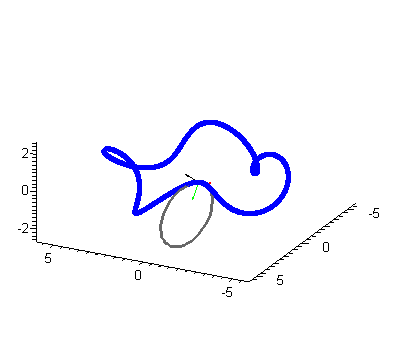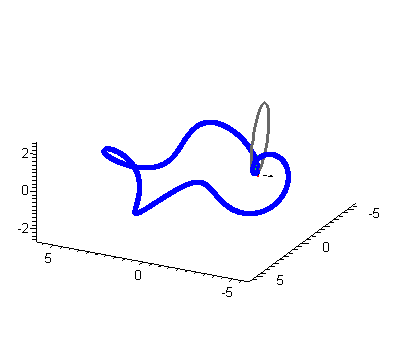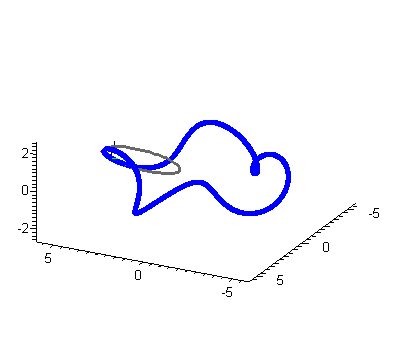
Here we construct the osculating circle (oscCt gives parametric equations at time t).
| > | r := t -> < xc(m*t,t,rL), yc(m*t,t,rL), zc(m*t,t,rL) >; |
![]()
![]()
| > | tnbFrame := TNBFrame(r(t),t):
kappa := Curvature(r(t),t): |
| > | Tt := tnbFrame[1]:
Nt := tnbFrame[2]: Bt := tnbFrame[3]: |
| > | oscCt := (cos(theta)/kappa)*Tt+(sin(theta)/kappa)*Nt+(1/kappa)*Nt+r(t): |
k_0 is the number of frames to generate for the animation.
NOTE: It may take a while to generate hundreds of frames.
To animate without displaying the torus, remove "t1" from
the "myAnimL ... display3d({....}...);" command below.
| > | k[0] := 150; |
![]()
| > | myAnimL := array(1..k[0]+1):
for t[0] from 0 by 1 to k[0] do PoscC := spacecurve(subs(t=(2*Pi/k[0])*t[0],oscCt),theta=0..2*Pi, color=black,thickness=2,scaling=constrained): PTt := arrow(subs(t=(2*Pi/k[0])*t[0],r(t)),subs(t=(2*Pi/k[0])*t[0],Tt), color=red,thickness=2): PNt := arrow(subs(t=(2*Pi/k[0])*t[0],r(t)),subs(t=(2*Pi/k[0])*t[0],Nt), color=yellow,thickness=2): PBt := arrow(subs(t=(2*Pi/k[0])*t[0],r(t)),subs(t=(2*Pi/k[0])*t[0],Bt), color=green,thickness=2): myAnimL[t[0]+1] := display3d({t1,c1,PoscC,PTt,PNt,PBt},scaling=constrained): end do: |
| > | display(seq(myAnimL[i],i=1..k[0]),insequence=true,scaling=constrained); |

| > | myAnimL2 := array(1..k[0]+1):
for t[0] from 0 by 1 to k[0] do PoscC := spacecurve(subs(t=(2*Pi/k[0])*t[0],oscCt),theta=0..2*Pi, color=black,thickness=2,scaling=constrained): PTt := arrow(subs(t=(2*Pi/k[0])*t[0],r(t)),subs(t=(2*Pi/k[0])*t[0],Tt), color=red,thickness=2): PNt := arrow(subs(t=(2*Pi/k[0])*t[0],r(t)),subs(t=(2*Pi/k[0])*t[0],Nt), color=yellow,thickness=2): PBt := arrow(subs(t=(2*Pi/k[0])*t[0],r(t)),subs(t=(2*Pi/k[0])*t[0],Bt), color=green,thickness=2): myAnimL2[t[0]+1] := display3d({t1,c1,PoscC,PTt,PNt,PBt},scaling=constrained, orientation=[45,-90*(sin((t[0]*Pi)/k[0]))+45]): end do: |
| > | display(seq(myAnimL2[i],i=1..k[0]),insequence=true,scaling=constrained); |
